Distributional Shift and Distributional Uncertainty

Why is distributional shift a problem?

Suppose we are trying to solve a specialised computer vision task, such as semantic segmentation of 10 classes in a given geographic location. We have a set of training images that allows us to get good performance for images that look similar to our training images, which are a tiny subset of the set of all natural images.

If we are interested in deploying a deep learning system into the real-world we can’t rely on the distribution of input data to remain the same as that of training. Therefore, we should be interested in the model performance over a broader distribution of test data, and determine the empirical performance over this broader distribution.

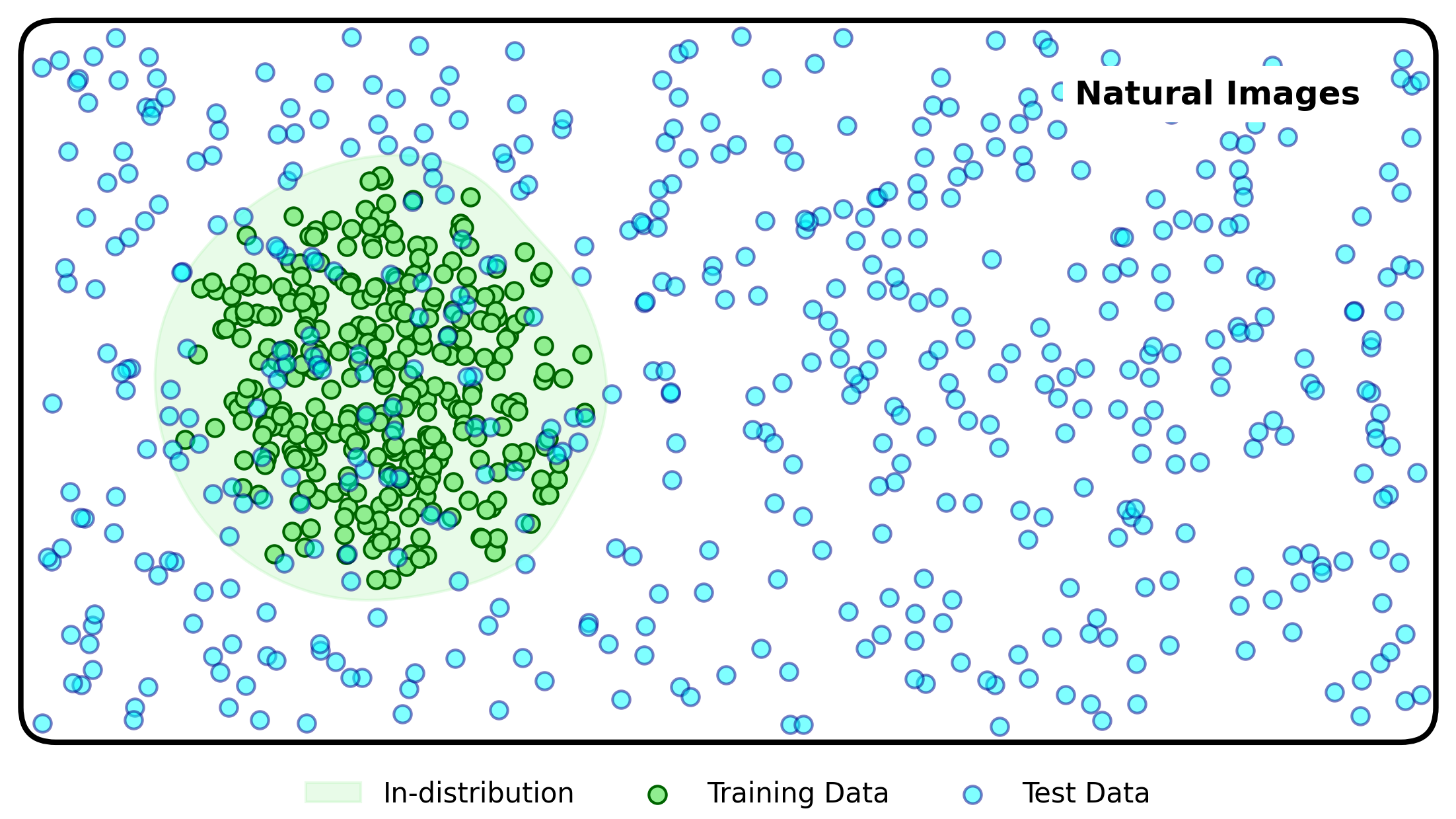
And what we observe is that a significant amount of test error is caused by the shift between the training and test datasets. We can describe this error as originating from distributional uncertainty.

To reduce or detect?

So given the presence of distributional uncertainty, how do we mitigate it in the scenarios where we care about ensuring safety? We have two options:

• Reduce the distributional uncertainty.
• Detect instances with high distributional uncertainty.

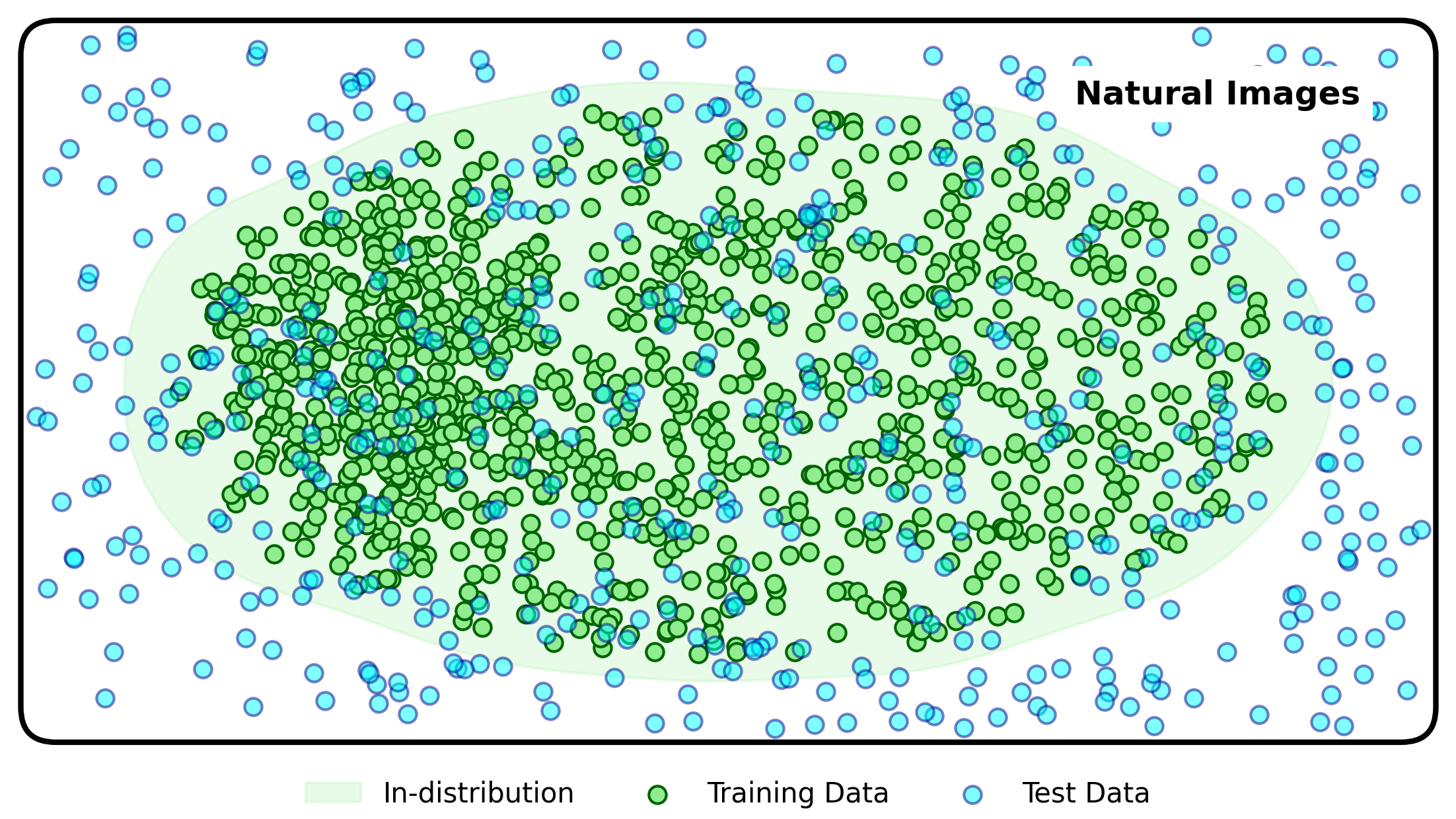
Reducing distributional uncertainty can be achieved by training on a much broader data distribution. This can include collecting and annotating large amounts of data (very costly), or using lots of unlabelled data in the form of unsupervised domain adaptation or foundation model training (perhaps costly in a different way).

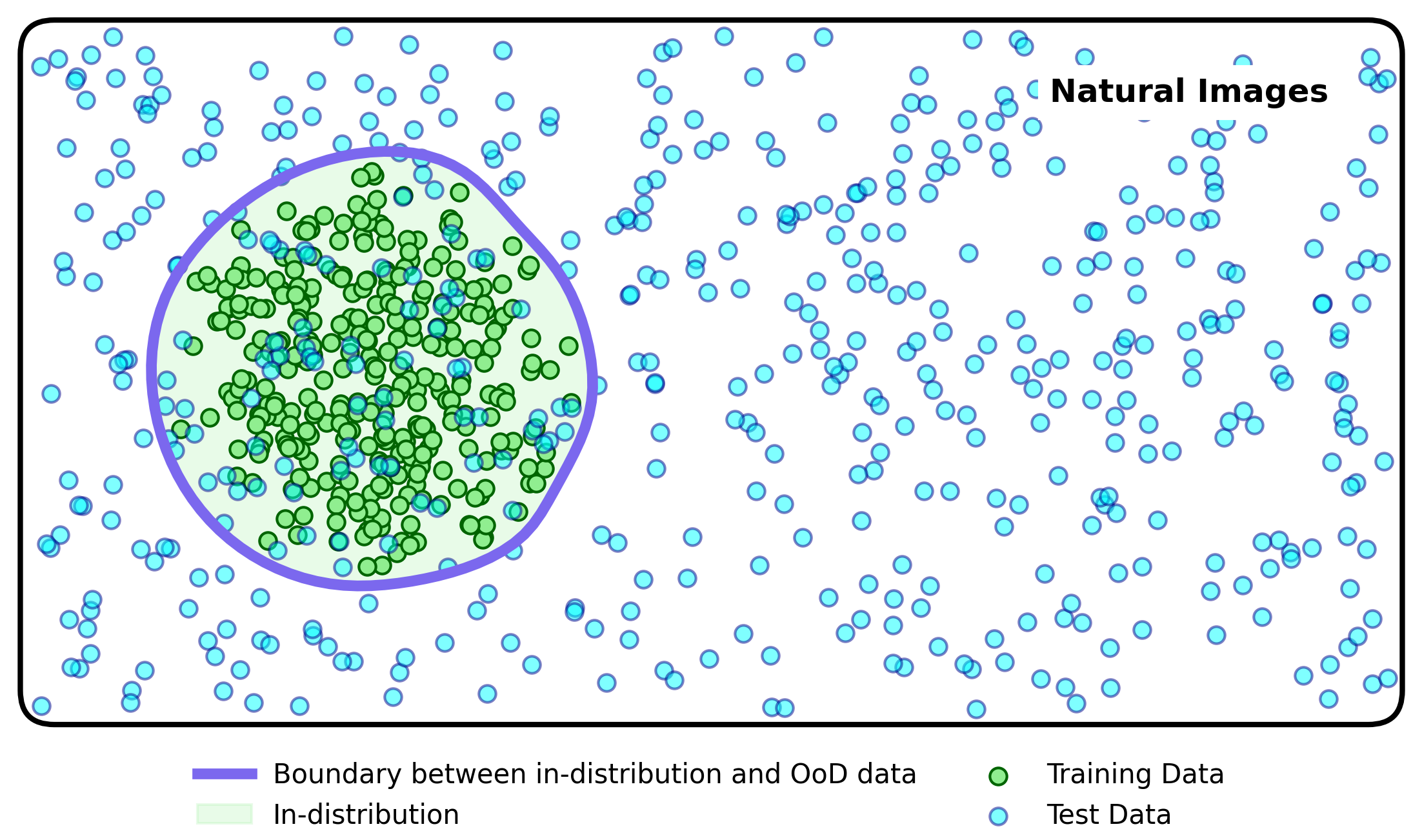
Detecting distributional uncertainty can be achieved by locating the boundary between what is similar to the training examples, and therefore in-distribution, and what is meaningfully distinct from the training examples, and is therefore out-of-distribution (OoD). Methods that do this are typically known as OoD detection or epistemic uncertainty estimation methods (more on this in this post).

Why is the detection of distributional uncertainty important?

In their essense, the reduction and detection of distributional uncertainty are orthogonal approaches for improving the safety of model deployment. Given the attention that training on large-scale datasets with large-scale neural networks gets, it is perhaps beneficial to focus on detection here.

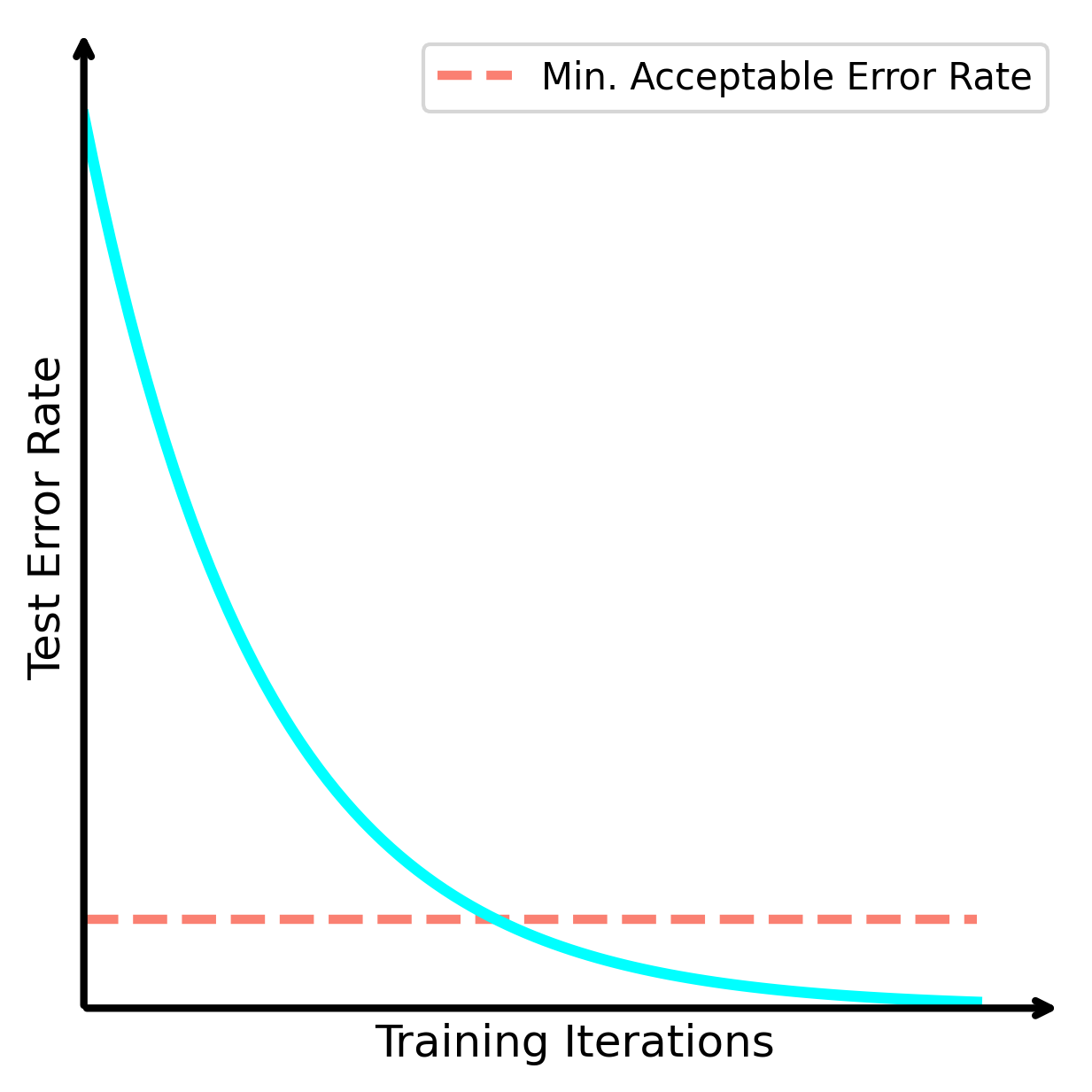
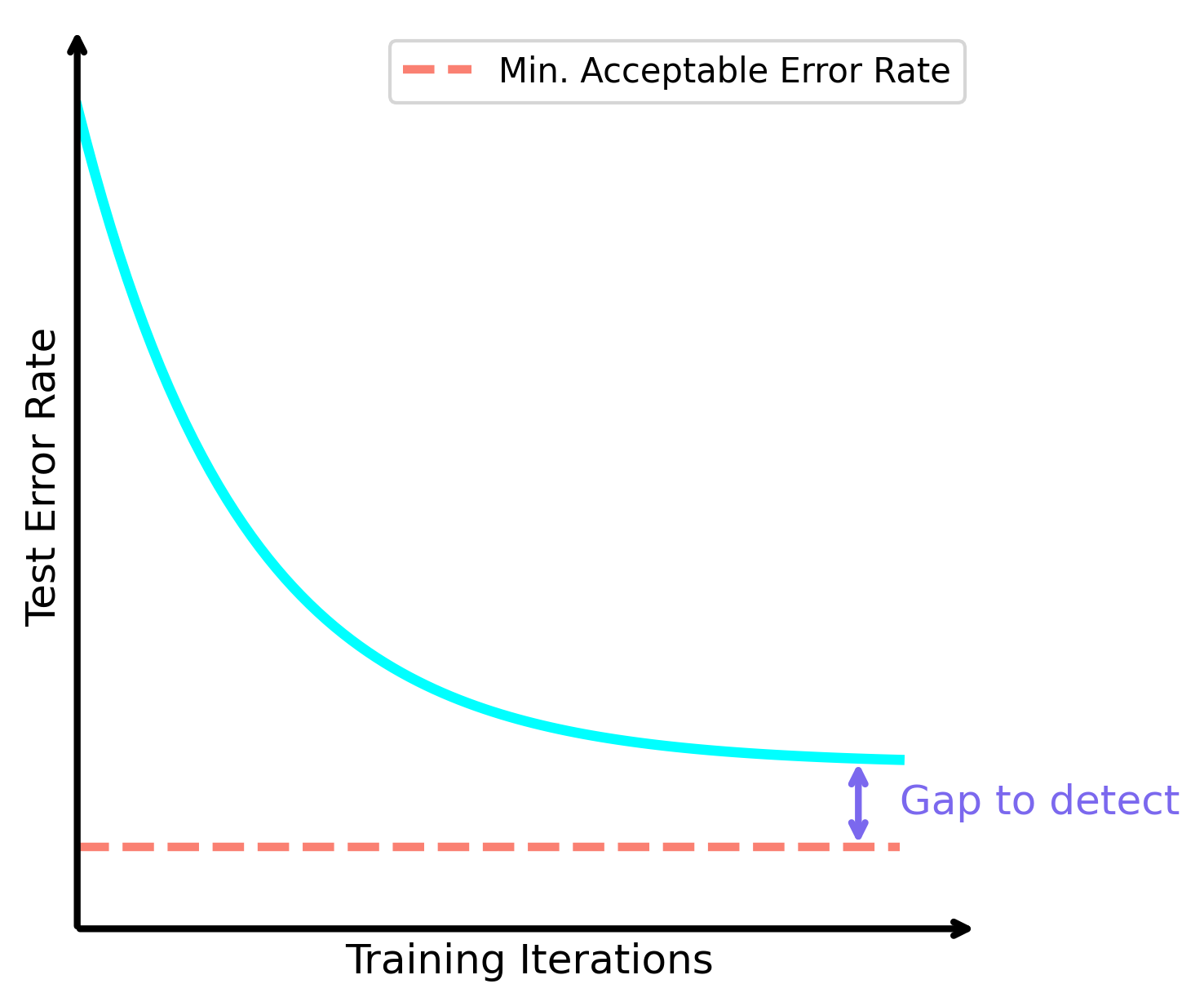
We can come up with a number of different factors, which cause it not to be possible to reduce distributional uncertainty to an appropriate level.

• Model Accuracy: even though large general models are very accurate on a broad range of tasks, for a specific narrow task, they do not beat a specialised version of themselves that is finetuned on this narrow task. The cost of this specialisation is an increase in distributional uncertainty.
• Compute Cost: smaller neural networks are less expressive, and so will perform well on a much narrower data distribution, and worse on everything else.
• Training Cost: sometimes training or finetuning a large model is needlessly expensive, and it is only economically or practically feasible to train a small model.

In these scenarios, high-quality distributional uncertainty estimation can be the key driver of getting useful models into the real-world.

Let me know if you have any thoughts about this: dswwilliamsworkspace@gmail.com